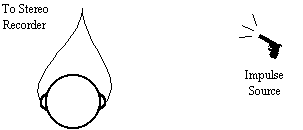
Gerry Beauregard, Michael Casey, Martin McKinney
Dartmouth College, 1991
Abstract
This paper describes experiments in which the acoustics of a small concert hall were simulated over headphones. Several techniques are described for obtaining Head Related Transfer Functions (HRTFs) from particular sound source locations to a specific listener position. These HRTFs were convolved with monophonic acoustically dry sounds. The result of such a convolution, when played over headphones, is a sound which has the general qualities of the of the hall in which the HRTF was measured, plus all the directional and distance cues of the HRTF. Applications to electro-acoustic music are discussed.
Introduction
The spatial quality of sound playback continues to be a concern of many researchers in the field of electro-acoustics. For example, there has been much work by John Chowning on utilizing space as a compositional parameter and many of his pieces reflect this concern. The experiments of (Schroeder 1979, 1980) although primarily concerned with 'live' acoustics, contain electro-acoustic models of acoustic listening situations. The concern for space in electro-acoustics extends back to the 1930's when the first successful stereo recording experiments were completed; the interest still holds today as research is being done on the role of three dimensional acoustic "visualization" in virtual reality applications (Fisher, Foster, Stone, Wenzel 1990).
Our group at Dartmouth College's Bregman Electronic Music Studio is interested in simulating real acoustic spaces for several reasons. The first reason is that we hope that sounds processed through HRTFs (Head Related Transfer Functions) obtained from real listening environments will sound more "real" than ones whose spatial qualities are determined using the normal studio techniques of panning to simulate side-to-side positioning, and varying reverb "wet-dry" ratio to simulate depth.
A second reason is to simulate over headphones what a piece of electro-acoustic music would sound like when played in a hall with particular speakers and speaker positions. This is a useful thing to be able to do, since a piece of music may sound very different when presented in an auditorium than when played over close-field studio monitors. Just as recording engineers for pop music try to mix songs to sound as good as possible over any playback equipment ranging from the most sophisticated home system to the cheapest portable AM radio, so too the composer of electro-acoustic music destined for "live" playback" should strive to make his mixes work well with many speaker/hall combinations.
The standard technique for obtaining a transfer function for a system is to generate an impulse response for that system. There are a number of different ways of approaching the problem of generating an impulse response. The methods we considered are outlined below.
Techniques for Obtaining HRTFs
Direct Measurement of the Impulse Response
The simplest method for obtaining the transfer function for a given sound source position and listener position is to record directly, using binaural microphones mounted on a dummy (in our case, a graduate student's) head, the response to a sound which approximates an impulse. Since an ideal impulse has a flat power spectrum (i.e. it has equal power at all frequencies), this "impulse response" contains all the information about the sound transmission characteristics between the source and the listener's ears (Atal 1966).
(Schroeder 1966) used this technique in his classic comparison of concert halls. Schroeder was attempting to address a problem that had been encountered by researchers attempting to correlate subjective listener preferences for concert halls with the physical characteristics of the halls. The basic problem is that in comparing concert halls, it would be desirable to switch quickly between the acoustic characteristics of several halls, while keeping all other conditions (such as the quality of performance, for example) the same. Since the halls of interest were spread over all of Europe, moving listeners between halls instantaneously was clearly impossible. Schroeder's technique, instead of bringing listeners to many halls, in effect brought many halls to the listeners.
Using a powerful spark gap as an impulse source, Schroeder obtained impulse responses for many well-known European concert halls. Recordings of an orchestra made in an anechoic chamber were then processed through these impulse responses. The results were then played back over loudspeakers in an anechoic chamber (after correction for cross-talk between speaker channels).
This basic method can be used with any sound source that approximates an impulse, such as a starter's pistol, cap gun, or even a hand clap. (The latter two were in fact used for some of our early tests with remarkably convincing results). While very simple, the method has its drawbacks. First of all, the typical impulse sources used do not produce pure impulses; a pure impulse is in fact impossible to create since it contains finite energy in an infinitely short time. The measured impulse response will therefore not be the true impulse response at all but will be distorted in ways depending on the exact nature of the source sound. The effect of this inaccuracy on sounds convolved with the impulse response will be a distortion of the frequency and phase characteristics. To complicate matters further, they are not even reproducible; a hand clap is probably the worst source in this respect. The directional qualities of these sources are very complicated (and again, not reproducible).
The direct impulse response measurement can also suffer from noise. Invariably concert halls have some background noise due to lighting and air conditioning. Noise in the microphones, cables, mic preamps, and recorder also contribute to noise in the measured impulse response. This noise is especially noticeable in the tail-end of the impulse response when the reverb of the hall has decayed to near inaudibility.
The standard way to minimize the effects of such noise is to average the measured impulse response over many trials. By doing this, the background noise will
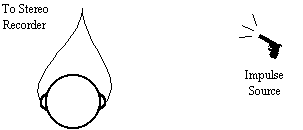
Figure 1: Simple method for getting impulse response.
tend to "cancel itself out" when averaged over many trials, while the desired response will be reinforced. This reinforcement, however, depends on the system's input signal — the impulse — being reproducible. Since spark gaps and starter pistols do not give reproducible impulses, averaging is not a practical way to minimize noise when these sources are used. The best one could do is turn off all the lights and ventilation, put the gain on the recorder as high as possible (without clipping), and not breathe while measurements are being taken.
Impulse Through Loudspeaker
If a loudspeaker and an electronically generated impulse is available then averaging can be used successfully. Such a scheme has been used by (Berman and Fincham 1977) to measure loudspeaker characteristics. A diagram of their method is shown in Figure 2. A pulse generator generates repetitive 10 Ás wide rectangular pulses which approximate ideal impulses over the frequency range of interest. The pulse is amplified and fed into a loudspeaker; a microphone picks up the acoustic response of the speaker. The interval between the pulses is chosen to be as short as possible with the provision that the residual sound from one impulse does not make a significant contribution to the next. The microphone signal is converted into digital form and added to a cumulative sum of responses. The pulse is also fed into the computer to act as a timing reference. After the desired number of responses have been obtained, the cumulative sum is divided by the number of responses measured.
What kind of improvement in signal to noise ratio (S/N) can we expect by averaging? If we assume that the background noise is totally uncorrelated, then if we add up the responses over n trials, the noise power will be proportional to n, whereas for the impulse response the amplitude will be proportional to n. Since power is proportional to the square of the signal amplitude, we would expect an improvement in S/N of vn. This means that averaging over 16 trials, for example, will give an improvement of 20log v16 = 12 dB. More generally, doubling the number of trials will give a 3 dB improvement in S/N.
As (Berman and Fincham 1977) point out, however, the actual S/N improvement will not be as large because the background noise will not generally be entirely uncorrelated. Care must therefore be taken to maximize the initial, non-averaged, S/N by eliminating background acoustic and electrical noise as much as possible, and by using as powerful an impulse as possible (without damaging the speaker).
If this technique is extended to measure

Figure 2: Fincham technique for loudspeaker impulse response measurement.
impulse response of a room, we of course end up lumping in the speaker impulse response as well. This may or may not be desirable, depending on how the impulse response is going to be used. If, as in our case, we want to simulate the effect of a sound playing through a loudspeaker in a hall, then this lumped response is precisely what we want.
Correlation Method
The correlation method for measuring the impulse response of an acoustic system is illustrated in Figure 3. The following description is adapted from that in (Ando 1985).
If si(t) is the system input and so(t) is the system output, the the cross-correlation between the input and output is given by:
where h(t) is the impulse response of the system, and fii(t) is the autocorrelation of the input signal.
If si(t) is a white noise signal with constant power spectrum N, then
fii(t) = N d(t)
Thus the equation for the cross-correlation becomes
fio(t) = N h (t)
and the impulse response is given by
h (t) = fio(t) / N
(Ando 1985) argues that external disturbances will not affect the measurement of h (t) since they will be uncorrelated with i(t) and therefore not contribute to fio (t).
Several dangers of using the correlation method must be pointed out, however. First of all, if si(t) is generated using a
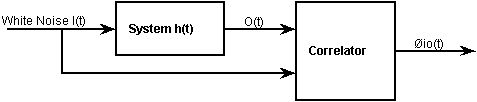
Figure 3: Correlation Method.
random process, then fii(t) will also be random for any particular realization of si(t). Although its expected value is Nd(t) as the duration approaches infinity, this will not be true for any particular finite length realization. Furthermore, external disturbances will contribute to fio(t), since for any finite length measurement the cross-correlation of the disturbance and si(t) will not be zero, although its expected value will be.
These facts become more salient if we switch to the frequency domain. Taking the Fourier transform for the expression for fio (t) gives
fio (w) = H(w) fii (w) ,
and since
fio (w) = Si(-w) So(w) (Lathi 1983),
we get
H(w) = fio (w) / fii (w)
= Si(-w) So(w) / Si(-w) Si(w)
= So(w) / Si(w)
Clearly if si(t) is random, then its spectrum Si(w) will be random as well, and could potentially be zero at some frequencies. An any good programmer knows, it's very dangerous to do divisions when the denominator may be zero! In addition, if so(t) contains some random external disturbance, it will add random error to So(w). The correlation method, then is equivalent to dividing one random variable by another!
The situation can be improved somewhat by generating si(t) in such a way that its spectrum is guaranteed to be flat. A method to do this is described later.
Using the correlation method and white noise as the system input can provide a better S/N ratio than the single impulse method, mainly because more energy can be put into the system since it can be spread over a longer time, and not because of any inherent noise-cancelling effects of the cross-correlation. In effect using white noise is the same as using a impulse in the sense that both signals have flat power spectra.
The best S/N ratio can be obtained by combining the use of noise as an input signal (to allow the greatest amount of energy to be put into the system) with signal averaging. This method is discussed in the next section.
The Cyclical Noise Method
(Berman and Fincham's 1977) method described above works well for measuring speaker impulse responses in part because the sound does not have to travel far. The speaker to microphone distance they used is under a meter, and therefore the speaker and microphone can be placed in a small, dead room. In measuring room responses, the speaker-microphone distance can easily be 10m or more. At that distance we cannot expect to get clean recordings of impulse responses since there are physical limits on the size of impulse one can put through a loudspeaker without damaging it.
One way to improve matters is to use a source signal which has the same flat Fourier transform as the impulse, but in which the power in the signal is spread over a longer time. One such signal is white noise. Clearly the response to such noise will not be the impulse response, but the impulse response can be obtained by deconvolution.
In a linear system, with impulse response h(t), the system output is related to the input by:
so(t) = si(t) * h(t)
where * is the convolution operator. Taking the Fourier transform of both sides gives
So(w) = Si(w) H(w)
The Fourier transform of the impulse response can therefore be obtained by dividing the transform of the output by the transform of the input.
H(w) = So(w) / Si(w)
h(t ) = F-1{ So(w) / Si(w) }
If the signal processing is done with discrete time (i.e. sampled) signals, as is the case if a digital computer is used, then the above relationship becomes
H[k] = So[k] / Si[k]
h[n] = IFFT ( H[k] )
where H[k], So[k], and Si[k] are the FFTs of the discrete time signals h[n], so[n] and si[n].
By dividing the FFT of the output by the FFT of the input, we are in effect doing a deconvolution of so[n] and si[n]. One interesting property of multiplying the FFTs of two signals is that it performs circular convolution of the two signals (Oppenheim 1975). Dividing FFTs therefore performs the inverse operation of circular deconvolution.
This property can be used to advantage if as input to the system we use cyclical noise, i.e. noise that repeats at regular intervals. After the first period of the noise, the system output will also be periodic, and averaging can therefore be performed on the output in the time domain as in (Berman and Fincham's 1977) method (see Figure 4). Dividing the FFT of the output signal, averaged over several periods, by the FFT of one period of the input signal will give the FFT of the impulse response, which can then be inverted to obtain the impulse response proper.
For this method to work, the period of the cyclical noise must be at least as long as the impulse response. In addition, the period must be a power of two number of samples long (this is a requirement of the FFT).
Convolution of a Dry Sound with the HRTF
Once the binaural HRTF (the impulse response for each ear for a given sound source location) is obtained for a specific sound source location and room, it can be convolved with an acoustically dry sound to give a result that, when listened to over headphones, sounds like the sound
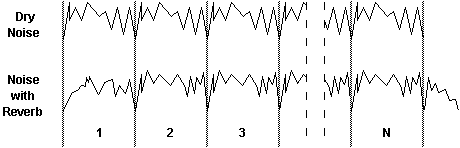
Figure 4: Response to Periodic Noise.
emanating from that specific location in he room. Using direct convolution to produce this result is a highly computational process. However, if the HRTF and the dry sound are transformed into the frequency domain using the FFT, they can simply be multiplied together and the result inversely transformed to obtain the result. Even with the computations involved in performing FFTs and inverse FFTs on both the HRTF and the dry sound, the number of computations for the latter method is only in the order of Nlog2N compared to N2 with direct convolution (where N is the number of points in both signals). Due to some properties of the FFT, however, there are some slight complications with using the FFT for convolution of two signals of varying lengths. We will now talk about these complications and how they are overcome.
Unlike the continuous time Fourier transformation method which can deal with periodic or non-periodic signals, the FFT method assumes that the signals are all periodic with the period being the length of the FFT. Thus multiplication and division operations on the FFTs of signals are analogous to circular convolution and deconvolution operations on their time domain counterparts respectively (Oppenheim 1975). (Although we speak of deconvolution theoretically, there is not a practical method of this operation in the time domain). In order to perform linear convolution using the FFT, the time domain signals must be padded with zeros until they are twice their original length before the FFT is taken. This eliminates the 'wrap-around' effects of circular convolution.
Another complication with using the FFT for the direct convolution of an HRTF with a dry sound, is that typically, the dry sound is much longer than the HRTF and an FFT of the length of the dry sound would be computationally cumbersome (if the length of the dry sound is known beforehand at all). A method called the overlap-and-save method can be employed to convolve two signals of unequal length (Oppenheim 1975). If two signals, h[n] of length N and x[m] of length M, where N is much shorter than M, are to be convolved, the convolution process can be done in sections of N points using FFTs of length 2N. Successive sections of N points are taken from x[m] and convolved with h[n] (by taking their FFTs, multiplying them together and taking the inverse FFT), each of which yields 2N points. The first N points of a section are added to the last N points of the previous section and so on until the end of x[m] is reached. Figure 5 shows this process. The top of the figure (a) shows h[n]. Figure (b) is x[m] divided into sections of N points. Figure (c) shows the placement (in time) of the sections (after the FFTs have been taken of both signals, the FFTs have been multiplied, and the inverse FFT has been taken) before they are added together. Figure (d) shows the final signal, the linear convolution of h[n] with x[m].
The Convolver program, listed in the Appendix, reads an HRTF data file and a dry sound file and convolves them using the overlap-and-save method described above.
Experiments and Results
All of our measurements were taken in Faulkner recital hall in the music department at Dartmouth College (see Figure 11). This space was used because of its convenient location and access rather than for any particular acoustic properties.
The basic method was to generate a set of HRTFs for the hall, by generating and recording impulses, and convolve them with a 'dry' test-sound. We qualitatively evaluated the results by comparing them to a recording of the same test-sound played back in the hall at the same position as for the impulse measurement. We were able to draw general
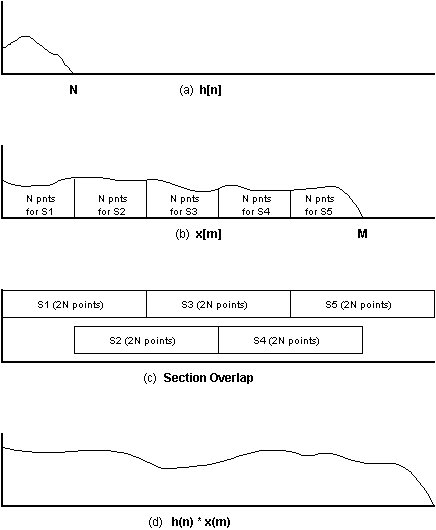
Figure 5: Overlap-and-Save method of Convolution.
conclusions about our method for generating HRTFs by listening, and as a result, our method changed during the experimental period.
In order to achieve maximal spatial effect in the results we used a pair of binaural microphones (Matsushita condenser cartridges modified by Len Moskowitz, Core Sound) which we were able to
Figure 6: Impulse Response Generated by a Starter Gun in Faulkner.
mount inside the test-subjects' ears. This method helped preserve some of the filtering that occurs due to the shape of the outer ear. Thus it was possible to generate HRTFs that effectively modelled cues for front and back as well as left and right directions. To preserve the relative intensity for different distances we calibrated the recording equipment by generating an impulse in close proximity to the subject and setting the recording level to obtain a peak level.
Generating the Impulse Response
The first method employed for generating impulses was a direct impulse measurement using a cap gun as a source. Recordings of the gun gave us a collection of impulse responses which we used to preliminarily evaluate the halls' acoustic properties and the effectiveness of our general method. Figure 6 shows an impulse response generated using this technique. This method gave us results which showed that obtaining an impulse response in this way was not entirely satisfactory for the purposes of this experiment. Comparative listening between results generated by different impulses showed that the difference in the sound each time the gun was fired significantly affected the result.
In order to get more consistent measurements, we switched to the cyclical noise method described earlier. The basic method was to generate a repeated nominal white noise burst of some fixed length; the noise consisted of a series of random numbers generated with the NoiseGen program. On the
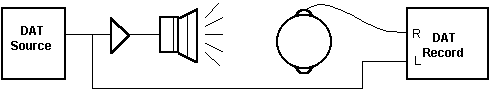
Figure 7: Experimental Setup using the Cyclical Noise Method.
basis of the lengths of the impulse responses measured using the cap gun, we determined that a period of 32K points for the noise would be adequate. The noise was then played through a loudspeaker in the hall. We used two DAT recorders: DAT1 (Panasonic SV3500) to play the noise and DAT2 (Panasonic SV255) to record the original noise directly from DAT1 for synchronization purposes, as well as the signal from one microphone (see Figure 7). Since we were only able to record the signal from one of the microphones at a time using this method, the subject had to remain absolutely still between successive noise bursts. The recorded channels were analyzed using the Correlator program (see Appendix) in order to obtain HRTFs for each ear.
The first results using the cyclical noise method were disappointing, and suggested several problems with our method. Apart from disadvantages arising from the inability to guarantee the same position of the subjects' head at each trial, we also experienced a large amount of unwanted noise in the final sound. We attempted to obtain an impulse response of the source noise through a wire in order to investigate the nature of the unwanted noise in more detail.
The following problems were discovered. The nominally white noise we were using turned out not to be white at all. Generating the samples using a pseudo-random number generator gave component frequencies whose amplitudes ranged over several orders of magnitude. This problem was overcome by writing a second noise generation program (NoiseGen2) which specified the amplitudes of the frequency components of the noise directly in the frequency domain. The phases of the components were randomized.
Another problem with the original noise was that it contained components at frequencies up to and including the Nyquist frequency. These upper components apparently could not be played or recorded properly by the DATs: when we did a simple analog transfer from one DAT to the other, an odd "amplitude-modulation" effect was observed. We hypothesized that this was due to the design of the reconstruction and anti-aliasing filters on the DATs: they simply were not designed to handle frequencies that close to the Nyquist frequency. Hence we further modified the noise generating and correlation programs to use band-limited noise. Thus our final source-noise had a uniform frequency distribution and was bandlimited to frequencies = 18KHz.
A third problem we found was that because the DAT sample clocks were not locked together, there was a significant drift in their relative phases. This drift proved to be problematic for the purposes of averaging over successive repetitions of the source signal (see Figure 8). The peak of the impulse response is reduced in amplitude and is spread out in time over successive averaging, which is equivalent to convolution with a rectangular pulse whose width depends on the amount of drift. The net effect is the same as that of low pass filtering the sound. Unfortunately because there was no way of locking the sample clocks on the DATs, while still using the microphone inputs on DAT2. This meant
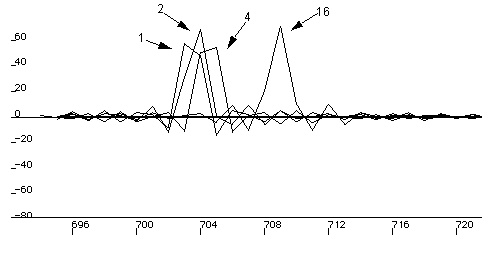
Figure 8: A series of impulse responses showing the effects of clock drift. Numbers
indicate which period of the recorded noise was used in its calculation.
that the anticipated gains in S/N from the use of the cyclical noise method could not be fully realized. Once these problems with the noise and the clock drift were understood and corrected as far as possible, we repeated our measurements, but using a somewhat different setup (see Figure 9). Since we were not concerned with the absolute time delay from speaker to listener, but we were concerned with the relative timing for the two ears, we decided not to bother with the direct connection from DAT1 to DAT2, and instead recorded both binaural microphones' signals into the two channels of DAT2 simultaneously.
Using this new setup and the modified noise, we were able to get fairly clean and convincing results (see Figure 10). While the residual noise in the impulse responses theoretically could have been reduced substantially by additional averaging, the drift in the DAT clocks made averaging over more than four cycles impossible.
Conclusions
While the final results of the experiments were not quite as good as me had originally hoped, the basic validity of our technique was confirmed. The most significant problems turned out to be unanticipated ones: 1) the fact that a good random number generator does not generate good noise, and 2) the fact that the sample clocks on the DATs were not nearly as accurate as we would have hoped. Nonetheless, the software that we wrote for this experiment was quite successful and the HRTFs that we obtained will be used in the future for electro-acoustic music composition.
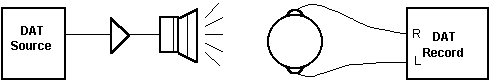
Figure 9: Final setup for the experiment.
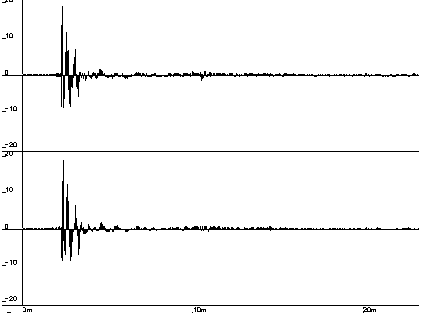
Figure 10: Impulse Response using the Cyclical Noise Method in Faulkner.
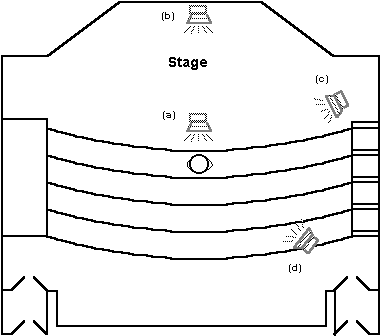
Figure 11: Floor plan of Faulkner Recital Hall showing speaker and listener positions for measurements taken during this study.
References
Ando, Y., 1985, Concert Hall Acoustics (Springer-Verlag, Berlin).
Atal, B.S., M.R. Schroeder, G.M.Sessler, and J.E.West, 1966, "Evaluation of Acoustic Properties of Enclosures by Means of Digital Computers", Journal of the Acoustical Society of America , vol. 40 no. 2.
Berman, J.M., and L.R.Fincham, 1977, "The Application of Digital Techniques to the Measurement of Loudspeaskers", Journal of the Audio Engineering Society, vol. 25 no. 6.
Lathi, B.P., 1983, Modern Digital and Analog Communications Systems (Holt, Rinehart and Winston, New York).
Oppenheim, A.V., and R.L. Schafer, 1975, Digital Signal Processing (Prentice-Hall, Englewood Cliffs, New Jersey).
Schroeder, M.R., 1978, Music Perception in Concert Halls , paper given at a seminar organized by the Committee for the Acoustics of Music in October 1978.
Wenzel, E.M., S.S. Fisher, P.K. Stone, and S.H. Foster, 1990, A System for Three-Dimensional Acoustic "Visualization" in a Virtual Environment Workstation , Proceeding of Visualization '90.
Appendix
Source code listings:
/*=======================================================================
Filename: Correlator.c
Language: C
Uses the correlation method to determine the impulse response of a
linear time-invariant system.
Given an input signal si[n] and an output signal so[n], this program
calculates
h[n] = IFFT { So[k] / Si[k] }
For this to work |Si[k]| must be non-zero for all k. Ideally |Si[k]| is flat,
i.e., si[n] is white noise or an impulse.
Modifications:
02/22/91 Gerry Beauregard Changed input file format. Now uses one file
for source and one for both channels of response.
Also got rid of temp files and just allocated
huge arrays, since memory space is not an issue
on the NeXT since it has virtual memory
02/05/91 Gerry Beauregard Uses two input files and computes left
and right impulse responses
02/05/91 Gerry Beauregard Added averaging over multiple segments
to improve S/N ratio
02/02/91 Gerry Beauregard Modified to use temporary files to reduce
amount of RAM needed.
01/28/91 Gerry Beauregard Modified to do two real FFTs simultaneously
by extracting conjugate symmetric and
anti-symmetric components
01/27/91 Gerry Beauregard Created this file
=========================================================================*/
/*=======================================================================
Includes
========================================================================*/
#include <math.h>
#include <stdlib.h>
#include <stdio.h>
#include "ComplexMath.h"
#include "FFT.h"
/*========================================================================
Constants
=========================================================================*/
#define TRUE 1
#define FALSE 0
#define MAX_16_BIT 65536
#define MAX_SAMPLE 32767
#define JUNK_SEGMENTS 2 /* Number of chunks of the input equal in
length to the noise period do we want to
ignore? (We have to ignore at least the
first to let the system reach a steady state
response) */
/*====================================================================
Typedefs
======================================================================*/
typedef struct
{
double L;
double R;
} Stereo;
/*================================================================
Prototypes
==================================================================*/
void main(void);
void UserInput(void);
int OpenFiles(void);
Stereo* ComputeImpulse(Stereo* inputArray, Stereo* outputArray, long numSamples);
Complex* ExtractLeft (Complex* array, long numSamples);
Complex* ExtractRight (Complex* array, long numSamples);
Stereo* ReadSDIIFile (FILE* theFile, long numSamples, long numSegments,
long junkSegments);
void WriteSDIIFile(FILE* theFile, Stereo* sampleArray, long numSamples);
void ScaleArray(Stereo* sampleArray, double scaleFactor, long numSamples);
void printArray(Complex* array, long N);
/*=================================================================
Global variables
==================================================================*/
char inputFileName [100];
char outputFileName[100];
char impulseFileName[100];
FILE* inputFile;
FILE* outputFile;
FILE* impulseFile;
long numSamples; /* Number of samples of input to use */
long numSegments; /* Number of segments to average over */
long zeroBins; /* High frequency bins to ignore */
Complex kZero = {0.0, 0.0};
/*--main------------------------------------------------------------
-------------------------------------------------------------------*/
void main(void)
{
Stereo* inputArray;
Stereo* outputArray;
Stereo* impulseArray;
UserInput();
if (OpenFiles() == TRUE)
{
inputArray = ReadSDIIFile(inputFile, numSamples, 1, 0);
outputArray = ReadSDIIFile(outputFile, numSamples, numSegments, JUNK_SEGMENTS);
impulseArray = ComputeImpulse(inputArray, outputArray, numSamples);
ScaleArray(impulseArray, MAX_SAMPLE, numSamples);
WriteSDIIFile(impulseFile, impulseArray, numSamples );
free(inputArray);
free(outputArray);
free(impulseArray);
fclose(inputFile);
fclose(outputFile);
fclose(impulseFile);
printf("Done!\n");
}
else
printf("Couldn't open files!\n");
} /* main */
/*--UserInput------------------------------------------------------------
Type out a cute message and gets some user input.
------------------------------------------------------------------*/
void UserInput(void)
{
long logNumSamples;
double sampleRate;
double cutoffFreq;
/* Message */
printf("\n");
printf("Correlator: Compute impulse response using correlation method\n");
printf("=============================================================\n");
printf("\n");
printf("by Gerry Beauregard 1991\n");
printf("\n");
/* Get number of points and segments */
printf("How many points per segment? ");
scanf("%ld", &numSamples);
logNumSamples = (long)( log( (double)numSamples - 0.001 ) / log(2.0) ) + 1;
numSamples = (long)(pow(2.0,(double)logNumSamples) + 0.01);
printf("Average over how many segments? ");
scanf("%ld", &numSegments);
/* Bandlimiting info */
printf("Sample rate? ");
scanf("%lf", &sampleRate);
printf("Cutoff frequency? ");
scanf("%lf", &cutoffFreq);
zeroBins = (int)( 0.5 + numSamples*(0.5*sampleRate-cutoffFreq)/sampleRate );
/* Get File names */
printf("Input (ie noise source file) file name? ");
scanf("%s", inputFileName);
printf("Output (ie room response) file name? ");
scanf("%s", outputFileName);
printf("Impulse response file name? ");
scanf("%s", impulseFileName);
} /* UserInput */
/*--OpenFiles------------------------------------------------------
Get input and output file names and make sure we can open them
-----------------------------------------------------------------*/
int OpenFiles(void)
{
int success;
success = TRUE;
inputFile = fopen(inputFileName, "r");
if (inputFile == NULL)
{
printf("Couldn't open %s\n", inputFileName);
success = FALSE;
}
outputFile = fopen(outputFileName, "r");
if (outputFile == NULL)
{
printf("Couldn't open %s\n", outputFileName);
success = FALSE;
}
impulseFile = fopen(impulseFileName, "w");
if (outputFile == NULL)
{
printf("Couldn't open %s\n", impulseFileName);
success = FALSE;
}
return success;
} /* OpenFiles */
/*--ComputeImpulse---------------------------------------------------------
Given arrays with the input and output, this function returns an array
with the impulse response (as computed by dividing the FFT of the output
by the FFT of the input, and doing an inverse FFT). Note: this function
screws up the contents of inputArray and outputArray!
-------------------------------------------------------------------------*/
Stereo* ComputeImpulse(
Stereo* inputArray,
Stereo* outputArray,
long numSamples)
{
long k; /* General purpose index */
long logNumSamples; /* Log2 of number of samples */
Complex* inputL; /* FFT of left channel of input */
Complex* inputR; /* FFT of right channel of input */
Complex* outputL; /* FFT of left channel of output */
Complex* outputR; /* FFT of right channel of output */
Complex* impulseL; /* Left channel impulse response */
Complex* impulseR; /* Right channel impulse response */
Stereo* impulse; /* Combined left and right impulse responses */
logNumSamples = (long)( log( (double)numSamples - 0.001 ) / log(2.0) ) + 1;
/* Allocate tons of space for arrays */
if ( ((inputL = (Complex*)calloc( numSamples, sizeof(Complex) ) ) == NULL)
|| ((inputR = (Complex*)calloc( numSamples, sizeof(Complex) ) ) == NULL)
|| ((outputL = (Complex*)calloc( numSamples, sizeof(Complex) ) ) == NULL)
|| ((outputR = (Complex*)calloc( numSamples, sizeof(Complex) ) ) == NULL)
|| ((impulseL = (Complex*)calloc( numSamples, sizeof(Complex) ) ) == NULL)
|| ((impulseR = (Complex*)calloc( numSamples, sizeof(Complex) ) ) == NULL)
|| ((impulse = (Stereo*) calloc( numSamples, sizeof(Stereo) ) ) == NULL) )
printf("Not enough memory to compute impulse response!\n");
else
{
/* Get FFTs of left and right parts of input */
FFT( (Complex*)inputArray, logNumSamples, FORWARD );
inputL = ExtractLeft ((Complex*)inputArray, numSamples );
inputR = ExtractRight((Complex*)inputArray, numSamples );
/* Get FFTs of left and right parts of output */
FFT( (Complex*)outputArray, logNumSamples, FORWARD );
outputL = ExtractLeft ((Complex*)outputArray, numSamples );
outputR = ExtractRight((Complex*)outputArray, numSamples );
/* Get FFT of impulse response by dividing output FFT by input FFT */
/* For bins outside frequency range of interest, set to zero */
impulseL[0] = kZero;
impulseR[0] = kZero;
for ( k = 1; k < numSamples; k++ )
{
if ( (k < numSamples/2-zeroBins) || (k > numSamples/2+zeroBins) )
{
impulseL[k] = CDiv( outputL[k], inputL[k] );
impulseR[k] = CDiv( outputR[k], inputR[k] );
}
else
{
impulseL[k] = kZero;
impulseR[k] = kZero;
}
}
/* Get impulse by inverse FFT of */
FFT( impulseL, logNumSamples, INVERSE);
FFT( impulseR, logNumSamples, INVERSE);
/* Combine impulses into a single stereo array */
for ( k = 0; k < numSamples; k++ )
{
impulse[k].L = impulseL[k].Re;
impulse[k].R = impulseR[k].Re;
}
}
/* Free all the temporary arrays */
free(inputL);
free(inputR);
free(outputL);
free(outputR);
free(impulseL);
free(impulseR);
return impulse;
}
/*--ExtractLeft------------------------------------------------------------
Extracts the frequency transformed data of left channel after using Gerry's
FFT function on a complex array with the left channel time data in the real
data's place and the right channel time data in the imaginary data's place.
(Conjugate symmetric and antisymmetric stuff).
----------------------------------------------------------------------*/
Complex* ExtractLeft(
Complex* array, /* Array with fresh (mixed) FFT data in it */
long numSamples)
{
Complex* left; /* Array for left channel FFT data */
long k;
/* allocate memory for extraction */
if ((left = (Complex*)calloc( numSamples,sizeof(Complex) )) == NULL)
printf("Not enough memory during ExtractLeft\n");
else
{
/* Extract FFT of Left Channel (real) part */
left[0].Re = array[0].Re;
left[0].Im = 0.0;
for (k = 1; k < numSamples; k++)
{
left[k].Re = (array[k].Re + array[numSamples-k].Re)/2.0;
left[k].Im = (array[k].Im - array[numSamples-k].Im)/2.0;
}
}
return left;
}
/*--ExtractRight------------------------------------------------------------
Extracts the frequency transformed data of right channel after using Gerry's
FFT function on a complex array with the left channel time data in the real
data's place and the right channel time data in the imaginary data's place.
(Conjugate symmetric and antisymmetric stuff).
----------------------------------------------------------------------*/
Complex* ExtractRight(
Complex* array, /* Array with fresh (mixed) FFT data in it */
long numSamples)
{
Complex* right; /* Array for right channel FFT data */
long k;
/* allocate memory for extraction */
if ((right = (Complex*)calloc( numSamples,sizeof(Complex) ) ) == NULL)
printf("Not enough memory during ExtractRight\n");
else
{
/* Extract FFT of Right Channel (imaginary) part */
right[0].Im = 0.0;
right[0].Re = array[0].Im;
for (k = 1; k < numSamples; k++)
{
right[k].Im = -(array[k].Re - array[numSamples-k].Re)/2.0;
right[k].Re = +(array[k].Im + array[numSamples-k].Im)/2.0;
}
}
return right;
}
/*--ReadSDIIFile--------------------------------------------------------
Reads the requested number of samples at the specified locations.
If not enough samples are available, it zero pads the array. The
input is assumed to be in the order left/right/left/right etc. Same
as ReadInputFile, except that the samples are assumed to be 16bit linear.
Averages samples for both channels over numSegments segments of numSamples.
Returns NULL if it cannot allocate array space.
-----------------------------------------------------------------------*/
Stereo* ReadSDIIFile(
FILE* theFile, /* File to read from */
long numSamples, /* Number of samples to read */
long numSegments, /* Number of segments to average over */
long junkSegments) /* Number of segments to ignore at start */
{
long j; /* Segment counter */
long k; /* Sample counter */
Stereo* sampleArray; /* Pointer to samples */
int upperByte, /* Upper and lower bytes of sample */
lowerByte;
int sampleL; /* Left channel */
int sampleR; /* Right channel */
sampleArray = (Stereo*)calloc( numSamples ,sizeof(Stereo) );
if (sampleArray != NULL)
{
/* Read and ignore junk segments */
for ( j = 0; j < junkSegments; j++ )
{
for ( k = 0; k < numSamples; k++ )
{
upperByte = fgetc(theFile);
lowerByte = fgetc(theFile);
upperByte = fgetc(theFile);
lowerByte = fgetc(theFile);
}
}
/* Start reading good stuff here */
for ( j = 0; j < numSegments; j++ )
{
for ( k = 0; k < numSamples; k++ )
{
upperByte = fgetc(theFile);
lowerByte = fgetc(theFile);
sampleL = upperByte*256 + lowerByte;
if (upperByte > 127)
sampleL -= MAX_16_BIT;
upperByte = fgetc(theFile);
lowerByte = fgetc(theFile);
sampleR = upperByte*256 + lowerByte;
if (upperByte > 127)
sampleR -= MAX_16_BIT;
sampleArray[k].L += (double) sampleL;
sampleArray[k].R += (double) sampleR;
}
}
for ( k = 0; k < numSamples; k++ )
{
sampleArray[k].L /= (double) numSegments;
sampleArray[k].R /= (double) numSegments;
}
}
rewind(theFile);
return sampleArray;
}
/*--WriteSDIIFile------------------------------------------------------
Takes a Stereo array and write it to a file in SDII format.
-----------------------------------------------------------------------*/
void WriteSDIIFile(
FILE* theFile,
Stereo* sampleArray,
long numSamples)
{
long k;
int upperByte;
int lowerByte;
for (k = 0; k < numSamples; k++)
{
/* Get left channel sample and divide it into bytes */
upperByte = ((int)sampleArray[k].L & 0xFF00) >> 8;
lowerByte = (int)sampleArray[k].L & 0x00FF;
/* Write left channel sample */
fputc( upperByte, theFile);
fputc( lowerByte, theFile);
/* Get right channel sample and divide into bytes */
upperByte = ((int)sampleArray[k].R & 0xFF00) >> 8;
lowerByte = (int)sampleArray[k].R & 0x00FF;
/* Write right channel sample */
fputc( upperByte, theFile);
fputc( lowerByte, theFile);
}
}
/*--ScaleArray---------------------------------------------------------
Multiplies every element by the specified number
-----------------------------------------------------------------------*/
void ScaleArray(
Stereo* sampleArray,
double scaleFactor,
long numSamples)
{
long k;
for ( k = 0; k < numSamples; k++ )
{
sampleArray[k].L *= scaleFactor;
sampleArray[k].R *= scaleFactor;
}
}
/*--PrintArray------------------------------------------------------------
-------------------------------------------------------------------------*/
void printArray(Complex* array, long N)
{
long k;
printf("Left\t\t\tRight\n");
for ( k = 0; k < N; k++ )
printf("%6lf\t\t\t%6lf\n", array[k].Re, array[k].Im);
}
/*=======================================================================
Filename: Convolver.c
Language: C
Uses the Overlap-Save method of convolution to convolve a 'dry' sound
with an impulse response.
Given an impluse response h[n] and a dry sound signal x[m], this program
calculates:
y[m] = IFFT { H[n] * X[m] }
Modifications:
02/07/91 Martin McKinney Created this file
=========================================================================*/
/*=======================================================================
Includes
========================================================================*/
#include <math.h>
#include <stdlib.h>
#include <stdio.h>
#include "ComplexMath.h"
#include "FFT.h"
/*========================================================================
Constants
=========================================================================*/
#define TRUE 1
#define FALSE 0
#define MAX_16_BIT 65536
#define MAX_SAMPLE 32767
/*====================================================================
Typedefs
======================================================================*/
typedef struct
{
double L;
double R;
} Stereo;
/*================================================================
Prototypes
==================================================================*/
void main(void);
void UserInput(void);
int OpenFiles(void);
void Convolve(void);
Stereo* ReadSDIIFile(FILE* InputFile, long N);
Complex* ExtractRight(Complex* array);
Complex* ExtractLeft(Complex* array);
void WriteSDIIFile(FILE* OutputFile, Stereo* OutBuf, long N);
void PrintArray(Complex* array, long N);
/*=================================================================
Global variables
==================================================================*/
char ImpulseFileName[100];
char SoundFileName[100];
char OutputFileName[100];
FILE* ImpulseFile;
FILE* SoundFile;
FILE* OutputFile;
long N; /* Number of samples of impulse */
long LogN; /* Used to make N a power of 2 */
long LogTwoN; /* Passed to FFT function */
int EndOfFile = 0;
int EndOfOperation = 0;
double lingain; /* Linear gain of impulse */
/*--main------------------------------------------------------------
-------------------------------------------------------------------*/
void main(void)
{
FILE* tempoutFileLeft;
FILE* tempoutFileRight;
UserInput();
if (OpenFiles() == TRUE)
{
printf ("Computing Output.....\n");
Convolve();
fclose(ImpulseFile);
fclose(SoundFile);
fclose(OutputFile);
}
printf ("Done!!\n");
}
/*--UserInput------------------------------------------------------------
Type out a cute message and gets some user input.
------------------------------------------------------------------*/
void UserInput(void)
{
double gain; /* gain of impulse resp. (in dB) */
/* Message */
printf("\n");
printf("Hello and welcome to Convolver, the program that likes you...\n");
printf("=============================================================\n");
printf("\n");
printf("by Martin McKinney and Gerry Beauregard 1991\n");
printf("\n");
/* Get impulse file name, number of points and gain */
printf("Impulse response file?\n");
scanf("%s", ImpulseFileName);
printf("How many points in the impulse response?\n");
scanf("%ld", &N);
LogN = (long)( log( (double)N - 0.001 ) / log(2.0) ) + 1;
N = (long)(pow(2.0,(double)LogN) + 0.01);
LogTwoN = (long)(log((double)(2*N) - 0.001)/log(2.0))+1;
printf("N = %ld\n", N);
printf("Gain of impulse response (in dB)?\n");
scanf("%lf", &gain);
lingain = pow(10.0,(gain/20.0));
/* Get other File names */
printf("Dry sound file?\n");
scanf("%s", SoundFileName);
printf("Output file?\n");
scanf("%s", OutputFileName);
} /* Blurb */
/*--OpenFiles------------------------------------------------------
Get input and output file names and make sure we can open them
-----------------------------------------------------------------*/
int OpenFiles(void)
{
int success;
success = TRUE;
ImpulseFile = fopen(ImpulseFileName, "r");
if (ImpulseFile == NULL)
{
printf("Couldn't open %s\n", ImpulseFileName);
success = FALSE;
}
SoundFile = fopen(SoundFileName, "r");
if (SoundFile == NULL)
{
printf("Couldn't open %s\n", SoundFileName);
success = FALSE;
}
OutputFile = fopen(OutputFileName, "w");
if (OutputFile == NULL)
{
printf("Couldn't open %s\n", OutputFileName);
success = FALSE;
}
return success;
} /* OpenFiles */
/*--Convolve------------------------------------------------------------
Convolves soundFile with impulseFile and puts the result in outputFile.
----------------------------------------------------------------------*/
void Convolve(void)
{
Stereo* OutBuf;
Stereo* ImpArray;
Stereo* SndArray;
Complex* ImpLeft; /* Pointer to H[k], left channel */
Complex* ImpRight; /* Pointer to H[k], right channel */
Complex* SndLeft; /* Pointer to S[k], left channel */
Complex* SndRight; /* Pointer to S[k], right channel */
Complex* Addend1Left; /* Pointer to first Addend, left */
Complex* Addend1Right; /* Pointer to first Addend, right */
Complex* Addend2Left; /* Pointer to second Addend, left */
Complex* Addend2Right; /* Pointer to second Addend, right */
Complex* Temp;
long k;
long section=0;
double maxpos=0; /* Maximum Positive Output Value */
double maxneg=0; /* Maximum Negative Output Value */
double peak=0; /* Peak Value of Output */
double linclip=0; /* Linear Clip Value */
double clip=0; /* Clip Value (in dB) */
/*** Allocate space for Addend Arrays ***/
if ((Addend1Left = (Complex*)calloc( 2*N,sizeof(Complex) ) ) == NULL)
printf("Not enough memory for Addend1Left\n");
if ((Addend1Right = (Complex*)calloc( 2*N,sizeof(Complex) ) ) == NULL)
printf("Not enough memory for Addend1Right\n");
if ((Addend2Left = (Complex*)calloc( 2*N,sizeof(Complex) ) ) == NULL)
printf("Not enough memory for Addend2Left\n");
if ((Addend2Right = (Complex*)calloc( 2*N,sizeof(Complex) ) ) == NULL)
printf("Not enough memory for Addend2Right\n");
if ((OutBuf = (Stereo*)calloc( N,sizeof(Stereo) ) ) == NULL)
printf("Not enough memory for OutBuf\n");
/*** Read impulse response, scale, take FFT, and extract left and right ***/
ImpArray = ReadSDIIFile(ImpulseFile, N);
if(EndOfFile == 1) /*Check to see if EOF was reached*/
{
EndOfFile = 0; /*Maybe do more with this later*/
printf("** ImpulseFile was shorter than %ld points **\n",N);
}
for (k=0; k<N; k++) /*Scale the Impluse Data*/
{
ImpArray[k].L = ImpArray[k].L * lingain /(double)MAX_SAMPLE;
ImpArray[k].R = ImpArray[k].R * lingain /(double)MAX_SAMPLE;
}
FFT ((Complex*)ImpArray, LogTwoN, FORWARD);
ImpLeft = ExtractLeft((Complex*)ImpArray);
ImpRight = ExtractRight((Complex*)ImpArray);
free(ImpArray);
ImpArray = NULL;
while(!EndOfOperation)
{
/*** Read a section of SoundFile,take FFT, and extract left and right ***/
SndArray = ReadSDIIFile(SoundFile, N);
FFT ((Complex*)SndArray, LogTwoN, FORWARD);
SndLeft = ExtractLeft((Complex*)SndArray);
SndRight = ExtractRight((Complex*)SndArray);
free(SndArray);
SndArray = NULL;
/*** Make Addend1 by multiplying H[k]*S[k] ***/
for (k=0; k<2*N; k++)
{
Addend1Left[k] = CMult(ImpLeft[k],SndLeft[k]);
Addend1Right[k] = CMult(ImpRight[k],SndRight[k]);
}
/*** Take IFFT of Addend1 ***/
FFT(Addend1Left, LogTwoN, INVERSE);
FFT(Addend1Right, LogTwoN, INVERSE);
/*** Add first N points of Addend1 to second N points of Addend2 ***/
/*** Output them to the output buffer. ***/
for (k=0; k<N; k++)
{
OutBuf[k].L = Addend1Left[k].Re + Addend2Left[N+k].Re;
OutBuf[k].R = Addend1Right[k].Re + Addend2Right[N+k].Re;
/*** Check values against peak values ***/
if (OutBuf[k].L > maxpos)
maxpos = OutBuf[k].L;
if (OutBuf[k].R > maxpos)
maxpos = OutBuf[k].R;
if (OutBuf[k].L < maxneg)
maxneg = OutBuf[k].L;
if (OutBuf[k].R < maxneg)
maxneg = OutBuf[k].R;
}
/*** Write the N points to the Output File ***/
WriteSDIIFile(OutputFile, OutBuf, N);
/*** If EOF was reached, output last part of Addend1. ***/
section++;
printf("Done with %ld sections\n", section);
if(EndOfFile == 1)
{
for (k=0; k<N; k++)
{
OutBuf[k].L = Addend1Left[N+k].Re;
OutBuf[k].R = Addend1Right[N+k].Re;
/*** Check values against peak values ***/
if (OutBuf[k].L > maxpos)
maxpos = OutBuf[k].L;
if (OutBuf[k].R > maxpos)
maxpos = OutBuf[k].R;
if (OutBuf[k].L < maxneg)
maxneg = OutBuf[k].L;
if (OutBuf[k].R < maxneg)
maxneg = OutBuf[k].R;
}
/*** Write the N points to the Output File ***/
WriteSDIIFile(OutputFile, OutBuf, N);
/*** Set peak, check against clipping, print warning ***/
if (fabs(maxneg) > maxpos)
peak = fabs(maxneg);
else peak = maxpos;
if (peak > (double)MAX_SAMPLE)
{
linclip = peak / (double)MAX_SAMPLE;
clip = 20.0*log10(linclip);
printf("******************************************\n");
printf("\n");
printf("*** Warning *** Clip on Output by %3.1lf dB\n",clip);
printf(" Repeat Procedure With Appropriate Gain\n");
printf("\n");
printf("******************************************\n");
}
/*** Terminate Operation ***/
printf("Got to end of operation\n");
EndOfOperation = 1;
}
/*** Else Switch Addend1 and Addend2 pointers and do it all again ***/
else
{
Temp = Addend2Left;
Addend2Left = Addend1Left;
Addend1Left = Temp;
Temp = Addend2Right;
Addend2Right = Addend1Right;
Addend1Right = Temp;
}
}
}
/*--ReadSDIIFile--------------------------------------------------------
Reads the requested number of samples into an array of twice that size
at the specified locations. If not enough samples are available, it zero
pads the array. The input is assumed to be in the order left/right/left
etc. Samples are assumed to be 16bit linear. The samples are read into
a Stereo array. Returns NULL if it allocate array space.
-----------------------------------------------------------------------*/
Stereo* ReadSDIIFile(
FILE* inputFile, /* File to read from */
long N) /* Number of samples to read */
{
long k; /* Sample counter */
Stereo* array; /* Pointer to samples */
int upperByte, /* Upper and lower bytes of sample */
lowerByte;
int sampleL; /* Left channel */
int sampleR; /* Right channel */
/*** Allocate twice as much space. This zero pads the array. ***/
if ((array = (Stereo*)calloc( 2*N,sizeof(Stereo) ) ) == NULL)
printf("Not enough memory during ReadSDIIFile\n");
else
{
for ( k = 0; k < N; k++ )
{
upperByte = fgetc(inputFile);
lowerByte = fgetc(inputFile);
sampleL = upperByte*256 + lowerByte;
if (upperByte > 127)
sampleL -= MAX_16_BIT;
if (lowerByte == EOF)
sampleL = 0;
upperByte = fgetc(inputFile);
lowerByte = fgetc(inputFile);
sampleR = upperByte*256 + lowerByte;
if (upperByte > 127)
sampleR -= MAX_16_BIT;
if (lowerByte == EOF)
sampleR = 0;
array[k].L = (double) sampleL;
array[k].R = (double) sampleR;
}
}
if((upperByte == EOF)||(lowerByte == EOF))
EndOfFile = 1;
return array;
}
/*--ExtractRight------------------------------------------------------------
Extracts the frequency transformed data of right channel after using Gerry's
FFT function on a complex array with the left channel time data in the real
data's place and the right channel time data in the imaginary data's place.
(Conjugate symmetric and antisymmetric stuff).
----------------------------------------------------------------------*/
Complex* ExtractRight(
Complex* array) /* Array with fresh (mixed) FFT data in it */
{
Complex* right; /* Array for right channel FFT data */
long k;
/* allocate memory for extraction */
if ((right = (Complex*)calloc( 2*N,sizeof(Complex) ) ) == NULL)
printf("Not enough memory during ExtractRight\n");
else
{
/* Extract FFT of Right Channel (imaginary) part */
right[0].Im = 0.0;
right[0].Re = array[0].Im;
for (k = 1; k < 2*N; k++)
{
right[k].Im = -(array[k].Re - array[(2*N)-k].Re)/2.0;
right[k].Re = +(array[k].Im + array[(2*N)-k].Im)/2.0;
}
}
return right;
}
/*--ExtractLeft------------------------------------------------------------
Extracts the frequency transformed data of left channel after using Gerry's
FFT function on a complex array with the left channel time data in the real
data's place and the right channel time data in the imaginary data's place.
(Conjugate symmetric and antisymmetric stuff).
----------------------------------------------------------------------*/
Complex* ExtractLeft(
Complex* array) /* Array with fresh (mixed) FFT data in it */
{
Complex* left; /* Array for left channel FFT data */
long k;
/* allocate memory for extraction */
if ((left = (Complex*)calloc( 2*N,sizeof(Complex) ) ) == NULL)
printf("Not enough memory during ExtractLeft\n");
else
{
/* Extract FFT of Left Channel (real) part */
left[0].Re = array[0].Re;
left[0].Im = 0.0;
for (k = 1; k < 2*N; k++)
{
left[k].Re = (array[k].Re + array[(2*N)-k].Re)/2.0;
left[k].Im = (array[k].Im - array[(2*N)-k].Im)/2.0;
}
}
return left;
}
/*--WriteSDIIFile------------------------------------------------------
Takes an array of N elements of Struct Stereo and writes them to the
specified output file in SoundDesignerII format.
-----------------------------------------------------------------------*/
void WriteSDIIFile(
FILE* OutputFile,
Stereo* OutBuf,
long N)
{
long k;
int upperByte;
int lowerByte;
for (k = 0; k < N; k++)
{
/* Get left channel sample and divide it into bytes */
upperByte = ((int)OutBuf[k].L & 0xFF00) >> 8;
lowerByte = (int)OutBuf[k].L & 0x00FF;
/* Write left channel sample */
fputc( upperByte, OutputFile);
fputc( lowerByte, OutputFile);
/* Get right channel sample and divide into bytes */
upperByte = ((int)OutBuf[k].R & 0xFF00) >> 8;
lowerByte = (int)OutBuf[k].R & 0x00FF;
/* Write right channel sample */
fputc( upperByte, OutputFile);
fputc( lowerByte, OutputFile);
}
}
/*--PrintArray------------------------------------------------------------
-------------------------------------------------------------------------*/
void PrintArray(Complex* array, long N)
{
long k;
printf("Left\t\t\tRight\n");
for ( k = 0; k < N; k++ )
printf("%12.8lf\t\t\t%12.8lf\n", array[k].Re, array[k].Im);
}
/*===============================================================================
Filename: FFT.h
Language: C
Modifications:
02/02/91 Gerry Beauregard Modified to calculate Wkn/N factors on the fly
instead of in advance in a table. Done to save
memory.
02/23/90 Gerry Beauregard Created this file
===============================================================================*/
#ifndef _FFT_H
#define _FFT_H
/*===================================================================
Constants
====================================================================*/
#define FORWARD 0
#define INVERSE 1
/*====================================================================
Prototypes
======================================================================*/
void FFT(Complex* X, long LogN, int Direction);
#endif
/*========================================================================
Filename: FFT.c
Language: C
FFT and associated functions.
Modifications:
02/02/91 Gerry Beauregard Switched to on-the-fly computation of Wkn/N
factors to reduce memory requirements.
02/23/90 Gerry Beauregard Created this file
=====================================================================*/
/*====================================================================
Includes
=====================================================================*/
#ifndef _STDIO_H
#include <stdio.h>
#endif
#ifndef _MATH_H
#include <math.h>
#endif
#ifndef _COMPLEXMATH_H
#include "ComplexMath.h"
#endif
#ifndef _H_FFT
#include "FFT.h"
#endif
/*========================================================================
Prototypes
==========================================================================*/
static void BitReverseArray(Complex* X, long LogN);
static long BitReverse(long Number, long Places);
/*=========================================================================
Globals
============================================================================*/
static double WAngleIncrement; /* Used in computation of Wkn/N factors */
/*--FFT---------------------------------------------------------------
Performs a decimation in frequency FFT or IFFT on an array of
complex numbers. Note that the output is in bit reversed order!
The arguments are:
X[] An array of Complex numbers. Used for input and
output.
LogN Log to base 2 of array size.
Direction The direction of the FFT.
These constants are useful for setting Direction:
FORWARD (0) Do forward FFT.
INVERSE (1) Do inverse FFT.
No return values. The output array is in the same variable as the input.
-----------------------------------------------------------------------*/
void FFT(Complex* X, long LogN, int Direction)
{
long Stage;
long FliesPerFFT; /* Number of butterflies per sub FFT */
long Span; /* Width of the butterfly */
long FFTStart; /* Starting index of sub FFT */
long FFTSpacing; /* Distance between start of sub FFTs */
long FlyCount; /* Counter for number of butterflies */
long Top,Bottom; /* Top and bottom index of a butterfly */
long k; /* General purpose index */
long N; /* Array size */
long WIndex; /* Index for Wkn/N factors */
long WIndexStep; /* Increment for index into WTable */
double XTopRe; /* = X[Top] */
double XTopIm;
register double XBotRe; /* = X[Bottom] */
register double XBotIm;
register double angle; /* Angle of Wkn/N factor */
register double WRe; /* Wkn/N factor */
register double WIm;
N = (long)(pow(2.0,(double)LogN) + 0.001);
if ( Direction == FORWARD )
WAngleIncrement = -2.0*PI/(double)N;
else
WAngleIncrement = +2.0*PI/(double)N;
FliesPerFFT = N >> 1; /* N/2 */
Span = N >> 1;
FFTSpacing = N;
WIndexStep = 1;
/* Put up a little scale to make it easy to monitor FFT's progress */
printf("FFT: ");
for ( Stage = 0; Stage < LogN; ++Stage )
printf("v");
printf("\n");
printf(" ");
fflush(stdout);
for ( Stage = 0; Stage < LogN; ++Stage )
{
FFTStart = 0;
for (FFTStart = 0; FFTStart < N; FFTStart += FFTSpacing)
{
WIndex = 0;
Top = FFTStart;
Bottom = Top + Span;
for (FlyCount = 0; FlyCount < FliesPerFFT; ++FlyCount)
{
angle = WAngleIncrement * WIndex;
WRe = cos(angle);
WIm = sin(angle);
XTopRe = X[Top].Re;
XTopIm = X[Top].Im;
XBotRe = X[Bottom].Re;
XBotIm = X[Bottom].Im;
X[Top].Re = XTopRe + XBotRe;
X[Top].Im = XTopIm + XBotIm;
XBotRe = XTopRe - XBotRe;
XBotIm = XTopIm - XBotIm;
X[Bottom].Re = XBotRe*WRe - XBotIm*WIm;
X[Bottom].Im = XBotRe*WIm + XBotIm*WRe;
++Top;
++Bottom;
WIndex += WIndexStep;
}
}
FliesPerFFT >>= 1; /* Divide by 2 by right shift */
Span >>= 1;
FFTSpacing >>= 1;
WIndexStep <<= 1; /* Divide by 2 by left shift */
/* Show progress */
printf("*");
fflush(stdout);
}
printf("\n");
/* The algorithm leaves the result in a scrambled order. This unscrambles it */
BitReverseArray(X,LogN);
/* Divide everything by N for IFFT */
if (Direction != FORWARD)
for (k = 0; k < N; k++)
{
X[k].Re = X[k].Re/(double)N;
X[k].Im = X[k].Im/(double)N;
}
/* printf("...Finished FFT\n"); */
}
/*--BitReverseArray-------------------------------------------------------
Takes array elements and puts them in bit-reversed order.
-------------------------------------------------------------------*/
void BitReverseArray(Complex* X, long LogN)
{
long Counter;
long BitReverseCounter;
long N;
Complex Temp;
N = (long)(pow(2.0,(double)LogN) + 0.0001);
for (Counter = 0; Counter < N; Counter++)
{
BitReverseCounter = BitReverse(Counter,LogN);
if (BitReverseCounter > Counter)
{
Temp = X[Counter];
X[Counter] = X[BitReverseCounter];
X[BitReverseCounter] = Temp;
}
}
}
/*--BitReverse-------------------------------------------------------
Do bit reversal of specified number of places of an long
-------------------------------------------------------------------*/
long BitReverse(long Number, long Places)
{
long i;
long Reverse;
Reverse = 0;
for (i = 0; i < Places; i++)
{
Reverse = Reverse << 1;
Reverse = Reverse | (Number & 0x0001);
Number = Number >> 1;
}
return Reverse;
}
/*======================================================================
Filename: ComplexMath.h
Language: Think C
Header file for complex math functions
Modifications:
02/23/90 Gerry Beauregard Created this file
01/27/91 Gerry Beauregard Modified to use floats instead
of doubles.
=======================================================================*/
#ifndef _COMPLEXMATH_H
#define _COMPLEXMATH_H
/*=====================================================================
Constants
=======================================================================*/
#define PI (3.14159265358979323846)
/*====================================================================
Typedefs
======================================================================*/
typedef struct
{
double Re;
double Im;
} Complex;
typedef struct
{
double Mag;
double Phase;
} Polar;
/*==================================================================
Prototypes
=====================================================================*/
Complex CAdd(Complex a, Complex b);
Complex CSub(Complex a, Complex b);
Complex CMult(Complex a, Complex b);
Complex CDiv(Complex a, Complex b);
Complex Conj(Complex a);
Polar ComplexToPolar(Complex x);
Complex PolarToComplex(Polar x);
double ComplexMag(Complex x);
double ComplexPhase(Complex x);
double RadToDeg(double x);
double DegToRad(double x);
#endif
/*=====================================================================
Filename: ComplexMath.c
Language: Think C
Source code for complex math functions
Modifications:
02/23/90 Gerry Beauregard Created this file
02/27/91 Gerry Beauregard Switch to floats from doubles
==========================================================================*/
/*=======================================================================
Includes
=========================================================================*/
#include <math.h>
#include "ComplexMath.h"
/*-- CAdd--------------------------------------------------------------
Complex addition
----------------------------------------------------------------------*/
Complex CAdd(Complex a, Complex b)
{
Complex Sum;
Sum.Re = a.Re + b.Re;
Sum.Im = a.Im + b.Im;
return Sum;
}
/*--CSub--------------------------------------------------------------
Complex subtraction
----------------------------------------------------------------------*/
Complex CSub(Complex a, Complex b)
{
Complex Difference;
Difference.Re = a.Re - b.Re;
Difference.Im = a.Im - b.Im;
return Difference;
}
/*--CMult--------------------------------------------------------------
Complex multiplication
----------------------------------------------------------------------*/
Complex CMult(Complex a, Complex b)
{
Complex Product;
Product.Re = a.Re*b.Re - a.Im*b.Im;
Product.Im = a.Re*b.Im + a.Im*b.Re;
return Product;
}
/*--CDiv--------------------------------------------------------------
Complex division
----------------------------------------------------------------------*/
Complex CDiv(Complex a, Complex b)
{
Polar PolarQuotient;
Complex Quotient;
PolarQuotient.Mag = ComplexMag(a)/ComplexMag(b);
PolarQuotient.Phase = ComplexPhase(a) - ComplexPhase(b);
Quotient = PolarToComplex(PolarQuotient);
return Quotient;
}
/*--Conj--------------------------------------------------------------
Complex conjugate
----------------------------------------------------------------------*/
Complex Conj(Complex a)
{
Complex Conjugate;
Conjugate = a;
Conjugate.Im *= -1.0;
return Conjugate;
}
/*--ComplexToPolar----------------------------------------------------
Conversion from rectangular to polar form
----------------------------------------------------------------------*/
Polar ComplexToPolar(Complex x)
{
Polar Result;
Result.Mag = ComplexMag(x);
Result.Phase = ComplexPhase(x);
return Result;
}
/*--PolarToComplex----------------------------------------------------
Conversion from polar to rectangular form
----------------------------------------------------------------------*/
Complex PolarToComplex(Polar x)
{
Complex Result;
Result.Re = x.Mag * cos(x.Phase);
Result.Im = x.Mag * sin(x.Phase);
return Result;
}
/*--ComplexMag----------------------------------------------------
Compute magnitude of complex number
----------------------------------------------------------------------*/
double ComplexMag(Complex x)
{
double Magnitude;
Magnitude = sqrt(x.Re*x.Re + x.Im*x.Im);
return Magnitude;
}
/*--ComplexPhase----------------------------------------------------
Compute the phase of a complex number
----------------------------------------------------------------------*/
double ComplexPhase(Complex x)
{
double Phase;
Phase = atan2(x.Im, x.Re);
return Phase;
}
/*--RadToDeg----------------------------------------------------
Convert radians to degrees
----------------------------------------------------------------------*/
double RadToDeg(double RadianPhase)
{
double DegreePhase;
DegreePhase = 360.0 * RadianPhase / (2.0 * PI);
return DegreePhase;
}
/*--DegToRad----------------------------------------------------
Convert degrees to radians
----------------------------------------------------------------------*/
double DegToRad(double DegreePhase)
{
double RadianPhase;
RadianPhase = 2.0 * PI * DegreePhase / 360.0;
return RadianPhase;
}